知名网站建设公司 北京国外产品推广平台

【附代码】判断线段是否相交算法（Python，C++）

作者：小猪快跑

基础数学&计算数学，从事优化领域5年+，主要研究方向：MIP求解器、整数规划、随机规划、智能优化算法

如有错误，欢迎指正。如有更好的算法，也欢迎交流！！！——@小猪快跑

相关文献

测试电脑配置

博主三千元电脑的渣渣配置：

CPU model: AMD Ryzen 7 7840HS w/ Radeon 780M Graphics, instruction set [SSE2|AVX|AVX2|AVX512]
Thread count: 8 physical cores, 16 logical processors, using up to 16 threads

基础

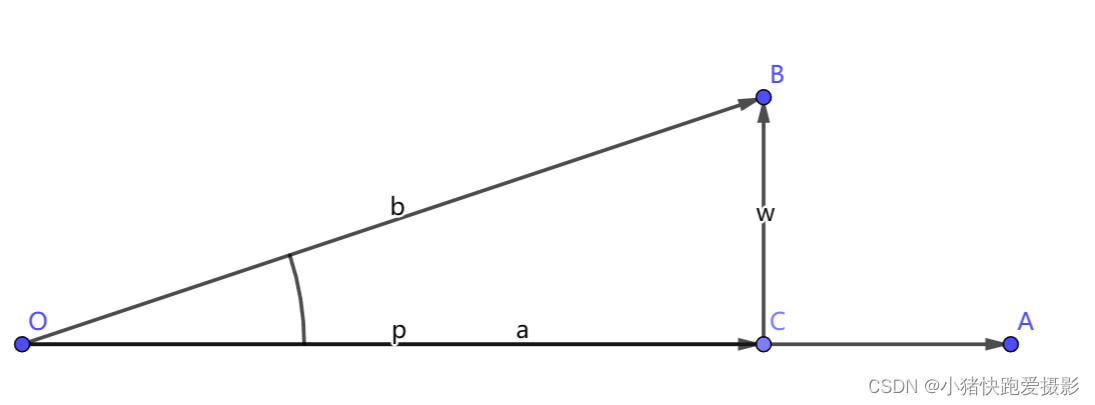
这里假设：
$$\begin{gathered} \overrightarrow{OA}=\vec{a}=(x_a,y_a) \\ \overrightarrow{OB}=\vec{b}=(x_b,y_b) \\ \overrightarrow{OC}=\vec{p}=(x_c,y_c) \\ \overrightarrow{CB}=\vec{w} \\ \angle AOB=\alpha \end{gathered}$$

向量旋转

任意向量都能表示成：
$$\left(\begin{array}{c}r\cos \alpha \\ r\sin \alpha \end{array}\right)$$
假设向量逆时针旋转了 $\beta$，那么我们容易知道旋转后向量是：
$$\left(\begin{array}{c}r\cos (\alpha +\beta )\\ r\sin (\alpha +\beta )\end{array}\right)$$
那么容易得到：
$$\left(\begin{array}{c}r\cos (\alpha +\beta )\\ r\sin (\alpha +\beta )\end{array}\right)=\left(\begin{array}{rr}\cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{array}\right)\left(\begin{array}{c}r\cos \alpha \\ r\sin \alpha \end{array}\right)$$
于是旋转向量就是：
$$\left(\begin{array}{rr}\cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{array}\right)$$

向量缩放

$$\left(\begin{array}{rr}r& 0\\ 0& r\end{array}\right)$$

向量投影

推导

主要利用 $\overrightarrow{OC}$ 和 $\overrightarrow{CB}$ 垂直，点积为0：
$$\begin{array}{r}\begin{array}{l}\vec{w}=\vec{b}-\vec{p}\\ \vec{w}\cdot \vec{p}=0\end{array}\}\Rightarrow (\vec{b}-\vec{p})\cdot \vec{p}=0\\ \vec{p}=k\vec{a}\end{array}\}\Rightarrow \begin{array}{r}(\vec{b}-k\vec{a})\cdot k\vec{a}=0\\ \vec{p}=k\vec{a}\end{array}\}\Rightarrow \vec{p}=\frac{\vec{a}\cdot \vec{b}}{\vec{a}\cdot \vec{a}}\vec{a}$$
那么投影矩阵
$$\begin{array}{lc}& P\vec{b}=\vec{p}=\vec{a}\frac{\vec{a}\cdot \vec{b}}{\vec{a}\cdot \vec{a}}\\ \Rightarrow & P=\frac{\vec{a}{\vec{a}}^T}{{\vec{a}}^T\vec{a}}\end{array}$$

点乘

点乘（Dot Product）的结果是点积，又称数量积或标量积（Scalar Product）

定义

$$\vec{a}\cdot \vec{b}=|\vec{a}||\vec{b}|\cos \alpha$$

推导

那么如何用解析几何来表示呢？

我们其实可以把 $\vec{a}$ 旋转 $\alpha$ 再缩放 $|\vec{b}|/|\vec{a}|$ 倍，就是 $\vec{b}$ 了：
$$\begin{array}{lc}& \left(\begin{array}{cc}\frac{|\vec{b}|}{|\vec{a}|}& 0\\ 0& \frac{|\vec{b}|}{|\vec{a}|}\end{array}\right)\left(\begin{array}{rr}\cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{array}\right)\left(\begin{array}{c}{x}_a\\ y_a\end{array}\right)=\left(\begin{array}{c}{x}_b\\ y_b\end{array}\right)\\ \Rightarrow & \left(\begin{array}{c}(x_a\cos \alpha -y_a\sin \alpha )|\vec{b}|\\ (x_a\sin \alpha +y_a\cos \alpha )|\vec{b}|\end{array}\right)=\left(\begin{array}{c}{x}_b|\vec{a}|\\ y_b|\vec{a}|\end{array}\right)\\ \Rightarrow & |\vec{a}||\vec{b}|\cos \alpha =x_a{x}_b+y_a{y}_b\end{array}$$

几何意义

点乘的结果表示 $\vec{a}$ 在 $\vec{b}$ 方向上的投影与 $\vec{b}$ 的乘积，反映了两个向量在方向上的相似度，结果越大越相似。基于结果可以判断这两个向量是否是同一方向，是否正交垂直，具体对应关系为：

1. $\vec{a}\cdot \vec{b}>0$ 则方向基本相同，夹角在0°到90°之间
2. $\vec{a}\cdot \vec{b}=0$ 则正交，相互垂直
3. $\vec{a}\cdot \vec{b}<0$ 则方向基本相反，夹角在90°到180°之间

叉乘

叉乘（Cross Product）又称向量积（Vector Product）。

定义

$$\vec{a}\times \vec{b}=|\vec{a}||\vec{b}|\sin \alpha$$

推导

那么如何用解析几何来表示呢？

我们其实可以把 $\vec{a}$ 旋转 $\alpha$ 再缩放 $|\vec{b}|/|\vec{a}|$ 倍，就是 $\vec{b}$ 了：
$$\begin{array}{lc}& \left(\begin{array}{cc}\frac{|\vec{b}|}{|\vec{a}|}& 0\\ 0& \frac{|\vec{b}|}{|\vec{a}|}\end{array}\right)\left(\begin{array}{rr}\cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{array}\right)\left(\begin{array}{c}{x}_a\\ y_a\end{array}\right)=\left(\begin{array}{c}{x}_b\\ y_b\end{array}\right)\\ \Rightarrow & \left(\begin{array}{c}(x_a\cos \alpha -y_a\sin \alpha )|\vec{b}|\\ (x_a\sin \alpha +y_a\cos \alpha )|\vec{b}|\end{array}\right)=\left(\begin{array}{c}{x}_b|\vec{a}|\\ y_b|\vec{a}|\end{array}\right)\\ \Rightarrow & |\vec{a}||\vec{b}|\sin \alpha =x_a{y}_b-x_b{y}_a\end{array}$$

几何意义

如果以向量 $\vec{a}$ 和 $\vec{b}$ 为边构成一个平行四边形，那么这两个向量外积的模长与这个平行四边形的面积相等。

判断线段是否相交

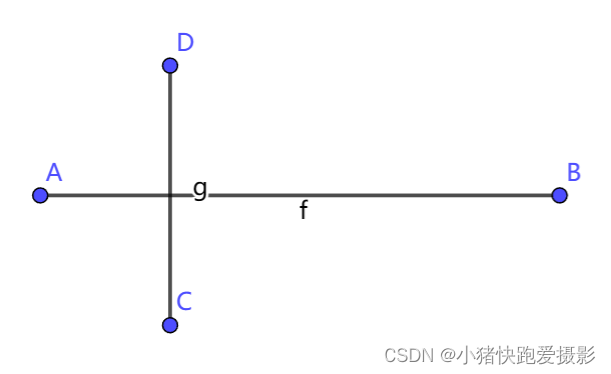
我们有了上面的基础后，其实思路就一下打开了！

其实我们只要想着 $\overrightarrow{AB}$ 的两边是 $C$ 和 $D$ ，那么也就是说 $\overrightarrow{AB}\times \overrightarrow{AD}$ 和 $\overrightarrow{AB}\times \overrightarrow{AC}$ 有正有负，同时呢 $\overrightarrow{CD}\times \overrightarrow{CA}$ 和 $\overrightarrow{CD}\times \overrightarrow{CB}$ 有正有负（这里要注意一下叉乘可能为0的情况，比如说 $A$ 在 $\overrightarrow{CD}$ 上）。这里我们有正有负采用直接判断而不是相乘小于零，这是因为相乘可能存在数值溢出等问题。而且一般的，和零的判断比乘法快很多。

我们直接上测试用例看看效果！！！

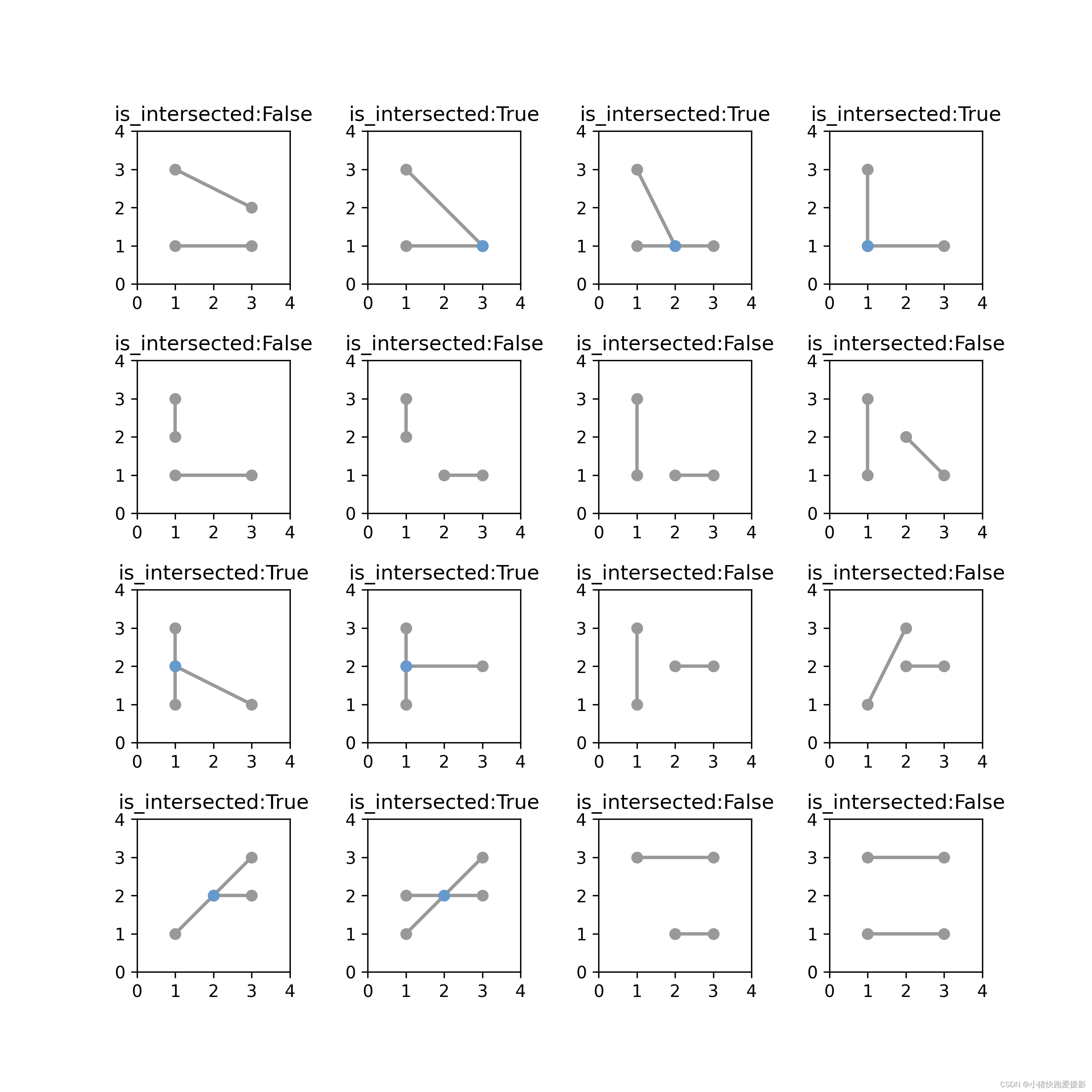
代码

C++

#include <iostream>
#include <chrono>using namespace std;int cross_product(int x1, int y1, int x2, int y2) {// 计算向量 (x1, y1) 和向量 (x2, y2) 的叉积return x1 * y2 - x2 * y1;
}int dot_product(int x1, int y1, int x2, int y2) {// 计算向量 (x1, y1) 和向量 (x2, y2) 的点乘return x1 * x2 + y1 * y2;
}bool is_intersected(int x1, int y1, int x2, int y2, int x3, int y3, int x4, int y4) {/*判断线段 (x1, y1)-(x2, y2) 和线段 (x3, y3)-(x4, y4) 是否相交AB×ACAB×ADCD×CACD×CB*/if ((max(x1, x2) < min(x3, x4)) or (max(x3, x4) < min(x1, x2)) or (max(y1, y2) < min(y3, y4)) or (max(y3, y4) < min(y1, y2))) {return false;}int abx = x2 - x1;int aby = y2 - y1;int acx = x3 - x1;int acy = y3 - y1;int adx = x4 - x1;int ady = y4 - y1;int bcx = x3 - x2;int bcy = y3 - y2;int cdx = x4 - x3;int cdy = y4 - y3;int cp1 = cross_product(abx, aby, acx, acy);int cp2 = cross_product(abx, aby, adx, ady);int cp3 = cross_product(cdx, cdy, -acx, -acy);int cp4 = cross_product(cdx, cdy, -bcx, -bcy);// 如果两个叉积的乘积小于0，则两个向量在向量 (x1, y1)-(x2, y2) 的两侧，即线段相交if (((cp1 > 0 and 0 > cp2) or (cp1 < 0 and 0 < cp2) or cp1 == 0 or cp2 == 0) and((cp3 > 0 and 0 > cp4) or (cp3 < 0 and 0 < cp4) or cp3 == 0 or cp4 == 0)) {return true;}return false;
}int test(int n) {int res = 0;for (auto x1 = 0; x1 < n; x1++) {for (auto y1 = 0; y1 < n; y1++) {for (auto x2 = 0; x2 < n; x2++) {for (auto y2 = 0; y2 < n; y2++) {if (x1 == x2 and y1 == y2) {continue;}for (auto x3 = 0; x3 < n; x3++) {for (auto y3 = 0; y3 < n; y3++) {for (auto x4 = 0; x4 < n; x4++) {for (auto y4 = 0; y4 < n; y4++) {if (x3 == x4 and y3 == y4) {continue;}res += is_intersected(x1, y1, x2, y2, x3, y3, x4, y4);}}}}}}}}return res;
}int main() {auto start = std::chrono::high_resolution_clock::now();std::cout << test(7) << std::endl;auto finish = std::chrono::high_resolution_clock::now();std::chrono::duration<double> elapsed = finish - start;std::cout << "Elapsed time: " << elapsed.count() << " s\n" << std::endl;return 0;
}

Python

from time import time
import math
from numba import njit@njit
def cross_product(x1, y1, x2, y2):"""计算向量 (x1, y1) 和向量 (x2, y2) 的叉积"""return x1 * y2 - x2 * y1@njit
def dot_product(x1, y1, x2, y2):"""计算向量 (x1, y1) 和向量 (x2, y2) 的点乘"""return x1 * x2 + y1 * y2@njit
def is_intersected(x1, y1, x2, y2, x3, y3, x4, y4):"""判断线段 (x1, y1)-(x2, y2) 和线段 (x3, y3)-(x4, y4) 是否相交AB×ACAB×ADCD×CACD×CB"""if (max(x1, x2) < min(x3, x4)) or (max(x3, x4) < min(x1, x2)) or (max(y1, y2) < min(y3, y4)) or (max(y3, y4) < min(y1, y2)):return Falseabx = x2 - x1aby = y2 - y1acx = x3 - x1acy = y3 - y1adx = x4 - x1ady = y4 - y1bcx = x3 - x2bcy = y3 - y2cdx = x4 - x3cdy = y4 - y3cp1 = cross_product(abx, aby, acx, acy)cp2 = cross_product(abx, aby, adx, ady)cp3 = cross_product(cdx, cdy, -acx, -acy)cp4 = cross_product(cdx, cdy, -bcx, -bcy)# 如果两个叉积的乘积小于0，则两个向量在向量 (x1, y1)-(x2, y2) 的两侧，即线段相交if ((cp1 > 0 > cp2) or (cp1 < 0 < cp2) or cp1 == 0 or cp2 == 0) and ((cp3 > 0 > cp4) or (cp3 < 0 < cp4) or cp3 == 0 or cp4 == 0):return Truereturn Falsedef test(n):res = 0for x1 in range(n):for y1 in range(n):for x2 in range(n):for y2 in range(n):if x1 == x2 and y1 == y2:continuefor x3 in range(n):for y3 in range(n):for x4 in range(n):for y4 in range(n):if x3 == x4 and y3 == y4:continueres += is_intersected(x1, y1, x2, y2, x3, y3, x4, y4)return resif __name__ == '__main__':s = time()print(test(7))print(time() - s)

画图代码

# main.py
import matplotlib.pyplot as plt
from shapely.geometry import Point, LineString, Polygon
from shapely.plotting import plot_polygon, plot_points, plot_linefrom csdn_line_intersect import is_intersected
from figures import BLUE, GRAY, set_limitsfig = plt.figure(1, figsize=(9, 9), dpi=300)
fig.subplots_adjust(wspace=0.5, hspace=0.5)  # 调整边距和子图的间距ax = fig.add_subplot(4, 4, 1)
x1, y1, x2, y2 = 1, 1, 3, 1
x3, y3, x4, y4 = 1, 3, 3, 2
a = LineString([(x1, y1), (x2, y2)])
b = LineString([(x3, y3), (x4, y4)])
plot_line(a, ax=ax, color=GRAY)
plot_line(b, ax=ax, color=GRAY)
plot_points(a.intersection(b), ax=ax, color=BLUE)
ax.set_title(f'is_intersected:{is_intersected(x1, y1, x2, y2, x3, y3, x4, y4)}')
set_limits(ax, 0, 4, 0, 4)ax = fig.add_subplot(4, 4, 2)
x1, y1, x2, y2 = 1, 1, 3, 1
x3, y3, x4, y4 = 1, 3, 3, 1
a = LineString([(x1, y1), (x2, y2)])
b = LineString([(x3, y3), (x4, y4)])
plot_line(a, ax=ax, color=GRAY)
plot_line(b, ax=ax, color=GRAY)
plot_points(a.intersection(b), ax=ax, color=BLUE)
ax.set_title(f'is_intersected:{is_intersected(x1, y1, x2, y2, x3, y3, x4, y4)}')
set_limits(ax, 0, 4, 0, 4)ax = fig.add_subplot(4, 4, 3)
x1, y1, x2, y2 = 1, 1, 3, 1
x3, y3, x4, y4 = 1, 3, 2, 1
a = LineString([(x1, y1), (x2, y2)])
b = LineString([(x3, y3), (x4, y4)])
plot_line(a, ax=ax, color=GRAY)
plot_line(b, ax=ax, color=GRAY)
plot_points(a.intersection(b), ax=ax, color=BLUE)
ax.set_title(f'is_intersected:{is_intersected(x1, y1, x2, y2, x3, y3, x4, y4)}')
set_limits(ax, 0, 4, 0, 4)ax = fig.add_subplot(4, 4, 4)
x1, y1, x2, y2 = 1, 1, 3, 1
x3, y3, x4, y4 = 1, 3, 1, 1
a = LineString([(x1, y1), (x2, y2)])
b = LineString([(x3, y3), (x4, y4)])
plot_line(a, ax=ax, color=GRAY)
plot_line(b, ax=ax, color=GRAY)
plot_points(a.intersection(b), ax=ax, color=BLUE)
ax.set_title(f'is_intersected:{is_intersected(x1, y1, x2, y2, x3, y3, x4, y4)}')
set_limits(ax, 0, 4, 0, 4)ax = fig.add_subplot(4, 4, 5)
x1, y1, x2, y2 = 1, 1, 3, 1
x3, y3, x4, y4 = 1, 3, 1, 2
a = LineString([(x1, y1), (x2, y2)])
b = LineString([(x3, y3), (x4, y4)])
plot_line(a, ax=ax, color=GRAY)
plot_line(b, ax=ax, color=GRAY)
plot_points(a.intersection(b), ax=ax, color=BLUE)
ax.set_title(f'is_intersected:{is_intersected(x1, y1, x2, y2, x3, y3, x4, y4)}')
set_limits(ax, 0, 4, 0, 4)ax = fig.add_subplot(4, 4, 6)
x1, y1, x2, y2 = 2, 1, 3, 1
x3, y3, x4, y4 = 1, 3, 1, 2
a = LineString([(x1, y1), (x2, y2)])
b = LineString([(x3, y3), (x4, y4)])
plot_line(a, ax=ax, color=GRAY)
plot_line(b, ax=ax, color=GRAY)
plot_points(a.intersection(b), ax=ax, color=BLUE)
ax.set_title(f'is_intersected:{is_intersected(x1, y1, x2, y2, x3, y3, x4, y4)}')
set_limits(ax, 0, 4, 0, 4)ax = fig.add_subplot(4, 4, 7)
x1, y1, x2, y2 = 2, 1, 3, 1
x3, y3, x4, y4 = 1, 3, 1, 1
a = LineString([(x1, y1), (x2, y2)])
b = LineString([(x3, y3), (x4, y4)])
plot_line(a, ax=ax, color=GRAY)
plot_line(b, ax=ax, color=GRAY)
plot_points(a.intersection(b), ax=ax, color=BLUE)
ax.set_title(f'is_intersected:{is_intersected(x1, y1, x2, y2, x3, y3, x4, y4)}')
set_limits(ax, 0, 4, 0, 4)ax = fig.add_subplot(4, 4, 8)
x1, y1, x2, y2 = 2, 2, 3, 1
x3, y3, x4, y4 = 1, 3, 1, 1
a = LineString([(x1, y1), (x2, y2)])
b = LineString([(x3, y3), (x4, y4)])
plot_line(a, ax=ax, color=GRAY)
plot_line(b, ax=ax, color=GRAY)
plot_points(a.intersection(b), ax=ax, color=BLUE)
ax.set_title(f'is_intersected:{is_intersected(x1, y1, x2, y2, x3, y3, x4, y4)}')
set_limits(ax, 0, 4, 0, 4)ax = fig.add_subplot(4, 4, 9)
x1, y1, x2, y2 = 1, 2, 3, 1
x3, y3, x4, y4 = 1, 3, 1, 1
a = LineString([(x1, y1), (x2, y2)])
b = LineString([(x3, y3), (x4, y4)])
plot_line(a, ax=ax, color=GRAY)
plot_line(b, ax=ax, color=GRAY)
plot_points(a.intersection(b), ax=ax, color=BLUE)
ax.set_title(f'is_intersected:{is_intersected(x1, y1, x2, y2, x3, y3, x4, y4)}')
set_limits(ax, 0, 4, 0, 4)ax = fig.add_subplot(4, 4, 10)
x1, y1, x2, y2 = 1, 2, 3, 2
x3, y3, x4, y4 = 1, 3, 1, 1
a = LineString([(x1, y1), (x2, y2)])
b = LineString([(x3, y3), (x4, y4)])
plot_line(a, ax=ax, color=GRAY)
plot_line(b, ax=ax, color=GRAY)
plot_points(a.intersection(b), ax=ax, color=BLUE)
ax.set_title(f'is_intersected:{is_intersected(x1, y1, x2, y2, x3, y3, x4, y4)}')
set_limits(ax, 0, 4, 0, 4)ax = fig.add_subplot(4, 4, 11)
x1, y1, x2, y2 = 2, 2, 3, 2
x3, y3, x4, y4 = 1, 3, 1, 1
a = LineString([(x1, y1), (x2, y2)])
b = LineString([(x3, y3), (x4, y4)])
plot_line(a, ax=ax, color=GRAY)
plot_line(b, ax=ax, color=GRAY)
plot_points(a.intersection(b), ax=ax, color=BLUE)
ax.set_title(f'is_intersected:{is_intersected(x1, y1, x2, y2, x3, y3, x4, y4)}')
set_limits(ax, 0, 4, 0, 4)ax = fig.add_subplot(4, 4, 12)
x1, y1, x2, y2 = 2, 2, 3, 2
x3, y3, x4, y4 = 2, 3, 1, 1
a = LineString([(x1, y1), (x2, y2)])
b = LineString([(x3, y3), (x4, y4)])
plot_line(a, ax=ax, color=GRAY)
plot_line(b, ax=ax, color=GRAY)
plot_points(a.intersection(b), ax=ax, color=BLUE)
ax.set_title(f'is_intersected:{is_intersected(x1, y1, x2, y2, x3, y3, x4, y4)}')
set_limits(ax, 0, 4, 0, 4)ax = fig.add_subplot(4, 4, 13)
x1, y1, x2, y2 = 2, 2, 3, 2
x3, y3, x4, y4 = 3, 3, 1, 1
a = LineString([(x1, y1), (x2, y2)])
b = LineString([(x3, y3), (x4, y4)])
plot_line(a, ax=ax, color=GRAY)
plot_line(b, ax=ax, color=GRAY)
plot_points(a.intersection(b), ax=ax, color=BLUE)
ax.set_title(f'is_intersected:{is_intersected(x1, y1, x2, y2, x3, y3, x4, y4)}')
set_limits(ax, 0, 4, 0, 4)ax = fig.add_subplot(4, 4, 14)
x1, y1, x2, y2 = 1, 2, 3, 2
x3, y3, x4, y4 = 3, 3, 1, 1
a = LineString([(x1, y1), (x2, y2)])
b = LineString([(x3, y3), (x4, y4)])
plot_line(a, ax=ax, color=GRAY)
plot_line(b, ax=ax, color=GRAY)
plot_points(a.intersection(b), ax=ax, color=BLUE)
ax.set_title(f'is_intersected:{is_intersected(x1, y1, x2, y2, x3, y3, x4, y4)}')
set_limits(ax, 0, 4, 0, 4)ax = fig.add_subplot(4, 4, 15)
x1, y1, x2, y2 = 2, 1, 3, 1
x3, y3, x4, y4 = 1, 3, 3, 3
a = LineString([(x1, y1), (x2, y2)])
b = LineString([(x3, y3), (x4, y4)])
plot_line(a, ax=ax, color=GRAY)
plot_line(b, ax=ax, color=GRAY)
plot_points(a.intersection(b), ax=ax, color=BLUE)
ax.set_title(f'is_intersected:{is_intersected(x1, y1, x2, y2, x3, y3, x4, y4)}')
set_limits(ax, 0, 4, 0, 4)ax = fig.add_subplot(4, 4, 16)
x1, y1, x2, y2 = 1, 1, 3, 1
x3, y3, x4, y4 = 1, 3, 3, 3
a = LineString([(x1, y1), (x2, y2)])
b = LineString([(x3, y3), (x4, y4)])
plot_line(a, ax=ax, color=GRAY)
plot_line(b, ax=ax, color=GRAY)
plot_points(a.intersection(b), ax=ax, color=BLUE)
ax.set_title(f'is_intersected:{is_intersected(x1, y1, x2, y2, x3, y3, x4, y4)}')
set_limits(ax, 0, 4, 0, 4)plt.savefig('output.png')
plt.show()

测试结果

C++: 0.0157648 s
Python(numba): 1.3376786708831787 s
Python(no numba): 3.585803985595703 s
Python(shapely): 73.45080494880676 s