沈阳做微网站的公司seo优化课程
目录
一、快速排序:
1、hoare(霍尔)版本:
2、挖坑法:
3、前后指针法:
4、非递归实现快速排序:
二、归并排序:
1、递归实现归并排序:
2、非递归实现归并排序:
三、排序算法整体总结:
一、快速排序:
基本思想:
任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
1、hoare(霍尔)版本:
运用递归原理,定义一个keyi(基准值),然后左找大,右找小,然后递归基准值的左右区间。
具体思路:
- 选定一个基准值,可以是a[0] / a[Size-1]。
- 确定两个指针 left 和 right 分别从左边和右边向中间遍历数组。
- 例如:选最左边的为基准值则right先走,遇到比基准值大的就停下,然后left走,遇到比基准值小的就停下,然后交换left与right位置对应的值。(如果以最右边为基准值,则left先走,right后走)
- 重复以上步骤,直到left = right ,最后将基准值与left(right)位置的值交换。
这样下来基准值所在的位置就是它排序后正确所在的位置,因为左边的所有数都比他小,右边的所有数都比他大。
然后再递归以基准值为界限的左右两个区间中的数,当区间中没有元素时,排序完成。
代码实现:
// 三数选中位数返回下标,作为一个快排的小优化,(不用也可以,不影响后面的代码)
int GetMedian(int* a, int begin, int end)
{int midi = (begin + end) / 2;// begin end midi三个数选中位数if (a[begin] < a[midi]){if (a[midi] < a[end])return midi;else if (a[begin] > a[end])return begin;elsereturn end;}else{if (a[end] > a[begin])return begin;else if (a[midi] > a[end])return midi;elsereturn end;}
}// hoare(霍尔)方法
int PartSort1(int* a, int begin, int end)// begin end 为下标
{int median = GetMedian(a, begin, end);// 选中位数返回下标swap(a[median], a[begin]); // 这里的swap使用的是库函数中写好了的,// 使用自己写的注意形参与实参int left = begin, right = end;int keyi = begin;while (left < right){// 右边找小while (left<right && a[right] >= a[keyi]){right--;}// 左边找大while (left < right && a[left] <= a[keyi]){left++;}swap(a[left], a[right]);}// 交换基准值和 left与right 交汇位置的值swap(a[left], a[keyi]);// 返回基准值的下标return left;
}void QuickSort(int* a, int begin, int end) // begin end 为下标
{if (begin >= end){return;}int keyi = PartSort1(a, begin, end); // 继续递归keyi(已排好序的值)的左右区间QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);
}2、挖坑法:
具体思路:
- 从最左边选定一个基准值取出,然后这个位置就为“坑”。
- 还是运用左右指针,当右指针遇到比基准值小的值时,将该值放入坑中,然后右指针指向的位置就是新的“坑”,然后移动左指针,当左指针遇到比基准值大的值时,同样将该值放入坑中,然后左指针指向的位置就是新的“坑”,然后再移动右指针,以此反复直到左右指针相遇。
- 当左右指针相遇时,将基准值放入最后的“坑”中。
然后再递归以基准值为界限的左右两个区间中的数,当区间中没有元素时,排序完成。
代码实现:
int PartSort1(int* a, int begin, int end)// begin end 为下标
{int median = GetMedian(a, begin, end);// 选中位数返回下标swap(a[median], a[begin]); // 这里的swap使用的是库函数中写好了的,// 使用自己写的注意形参与实参int left = begin, right = end;int keyi = begin;while (left < right){// 右边找小while (left<right && a[right] >= a[keyi]){right--;}// 左边找大while (left < right && a[left] <= a[keyi]){left++;}swap(a[left], a[right]);}// 交换基准值和 left与right 交汇位置的值swap(a[left], a[keyi]);// 返回基准值的下标return left;
}// 挖坑法
int PartSort2(int* a, int begin, int end)
{int median = GetMedian(a, begin, end);// 选中位数返回下标swap(a[median], a[begin]); // 这里的swap使用的是库函数中写好了的,// 使用自己写的注意形参与实参// 定义基准值与“坑位”int keyi = a[begin];int hole = begin;// begin 与 end 充当左右指针while (begin < end){// 右边找小,填到左边的坑while (begin < end && a[end] >= keyi){end--;}// 填坑a[hole] = a[end];hole = end;// 左边找大,填到右边的坑while (begin < end && a[begin] <= keyi){begin++;}// 填坑a[hole] = a[begin];hole = begin;}a[hole] = keyi;return hole;
}void QuickSort(int* a, int begin, int end) // begin end 为下标
{if (begin >= end){return;}int keyi = PartSort2(a, begin, end); // 继续递归keyi(已排好序的值)的左右区间QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);
}3、前后指针法:
具体思路:
- 定义一个基准值key,指针 prev 和 cur。(cur = prev + 1)
- cur先走,遇到比key大的值,++cur。
- cur遇到比key小的值,++prev,交换prev和cur位置的值。
- 以此反复直到cur走出数组范围。
最后交换key和prev的值
然后再递归以基准值为界限的左右两个区间中的数,当区间中没有元素时,排序完成。
代码实现:
int PartSort3(int* a, int begin, int end)
{int median = GetMedian(a, begin, end);// 选中位数返回下标swap(a[median], a[begin]); // 这里的swap使用的是库函数中写好了的,// 使用自己写的注意形参与实参// 定义基准值、前后指针int keyi = begin;int prev = begin, cur = prev + 1;while (cur <= end){// 保留keyi下标的值if (a[cur] < a[keyi] && ++prev != cur)// 避免自己给自己赋值的情况,{swap(a[prev], a[cur]);}++cur;}swap(a[prev], a[keyi]);// 因为交换了位置,所以下标prev的位置才是基准值return prev;
}void QuickSort(int* a, int begin, int end) // begin end 为下标
{if (begin >= end){return;}int keyi = PartSort3(a, begin, end); // 继续递归keyi(已排好序的值)的左右区间QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);
}4、非递归实现快速排序:
非递归实现快速排序就需要运用到栈,栈中存放的是需要排序的左右区间。其大致思想是与递归实现的思路类似。
具体思路:
- 将待排序数组的左右下标入栈。
- 若栈不为空,分两次取出栈顶元素,分为闭区间的左右界限。
- 将区间中的元素按照【上述三种方法(霍尔、挖坑、前后指针)的任意一种】得到基准值的位置
- 再以基准值为界限,当基准值左右区间中有元素,将区间入栈
然后重复上述步骤直到栈中没有元素时,排序完成。
代码实现:
void QuickSortNonr(int* a, int begin, int end)
{// 这里使用的是C++标准模板库的stack,如果是C语言的话需手搓一个栈出来// 但基本的思路是一样的,这里为了方便就不手搓哩// 定义一个栈并初始化stack<int> s;// 将数组的左右下标入栈s.push(end);s.push(begin);// 当栈不为空时,继续排序while (!s.empty()){int left = s.top();s.pop();int right = s.top();s.pop();// 获取基准值的位置(下标)int keyi = PartSort1(a, left, right);// [left, keyi-1] keyi [keyi+1, right]// 以基准值为界限,若基准值左右区间中有元素,则将区间入栈if (left < keyi - 1){s.push(keyi - 1);s.push(left);}if (keyi + 1 < right){s.push(right);s.push(keyi + 1);}}// 如果是手搓的栈,记得释放内存
}快速排序的特性总结:
快速排序整体的综合性能和使用场景都是比较好的。
时间复杂度:O(N*logN)
空间复杂度:O(logN)
稳定性:不稳定
二、归并排序:
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,采用分治法(Divide and Conquer)的一个非常典型的应用。
基本思想:
将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
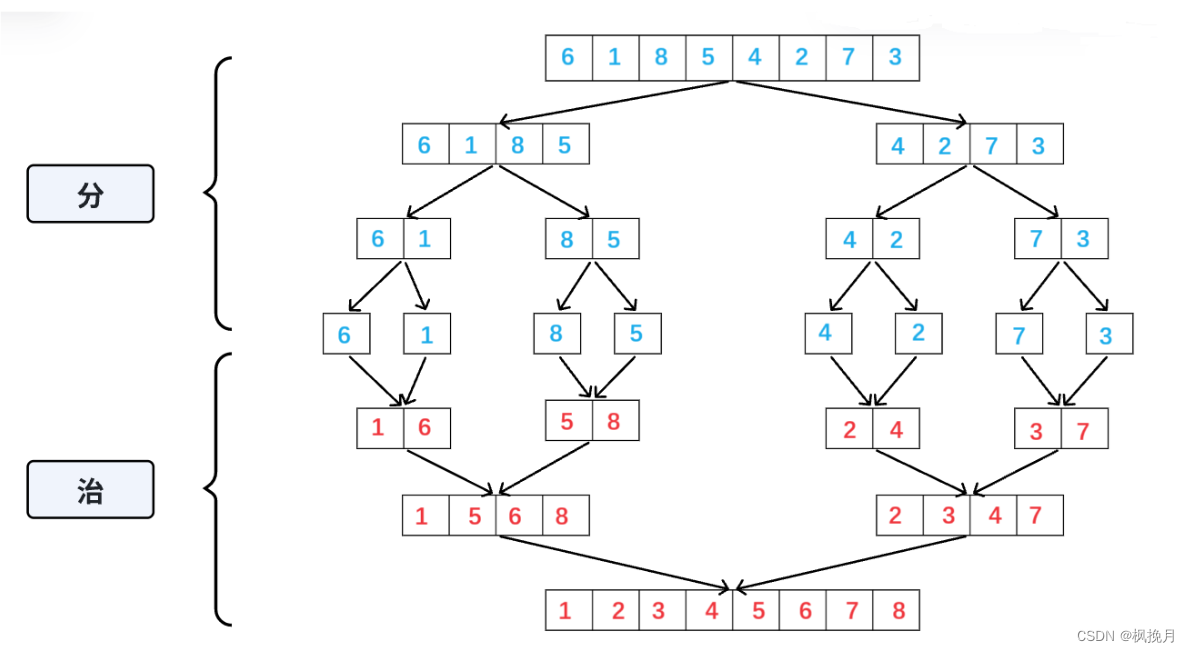
本质为:
依次将数组划分,直到每个序列中只有一个数字。一个数字默认有序,然后再依次合并排序。
1、递归实现归并排序:
代码实现:
void _MergeSort(int* a, int begin, int end, int* tmp)
{// 当区间中没有元素时将不再进行合并if (begin >= end){return;}// 划分数组,进行递归操作int mid = (begin + end) / 2;_MergeSort(a, begin, mid, tmp); // 划分左区间_MergeSort(a, mid + 1, end, tmp); // 划分右区间// 两个有序序列进行合并int begin1 = begin, end1 = mid;int begin2 = mid + 1, end2 = end;int i = begin;while (begin1 <= end1 && begin2 <= end2)// 结束条件为一个序列为空就停止。{if (a[begin1] < a[begin2]){tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}// 进行上一步的操作后会有一个有序序列不为空,将其合并进tmpwhile (begin1 <= end1){tmp[i++] = a[begin1++];}while (begin2 <= end2){tmp[i++] = a[begin2++];}//将合并后的序列拷贝到原数组中memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));}void MergeSort(int* a, int Size)
{//因为需要将两个有序序列进行合并,所以需要开辟相同空间int* tmp = (int*)malloc(sizeof(int) * Size);assert(tmp);_MergeSort(a, 0, Size - 1, tmp);free(tmp);
}2、非递归实现归并排序:
非递归实现的思想与递归实现的思想是类似的,但序列划分过程和递归是相反的,并不是每次一分为二, 而是先拆分为一个元素一组、再两个元素一组进行排序、再四个元素一组进行排序....以此类推,直到将所有的元素排序完。
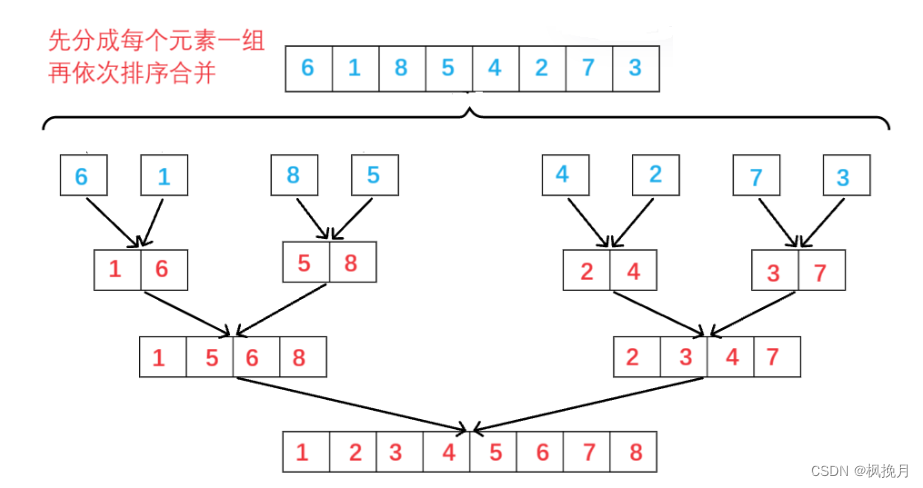
代码实现:
void MergeSortNonR(int* a, int Size)
{int* tmp = (int*)malloc(sizeof(int) * Size);assert(tmp);// 先将元素拆为一个一组int gap = 1;while (gap < Size) // 当gap=Size时就是一组序列{// 每两组进行一个合并排序int index = 0; // 记录tmp数组中元素的下标for (int i = 0; i < Size; i += 2 * gap)// 两组中元素的个数为2*gap{// 控制两组的边界int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;// 当原数组中元素个数不是2^n时,最后两组会出现元素不匹配的情况// 情况1: 当 end1 >= Size 或 begin2 >= Size 时即最后两组元素只剩下一组时不需要进行合并排序if (end1 >= Size || begin2 >= Size){break;}// 情况2: end2 >= Size 时,即最后两组中,第二组的元素个数小于第一组,则需要调整第二组的边界if (end2 >= Size){end2 = Size - 1;}// 进行合并排序while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[index++] = a[begin1++];}else{tmp[index++] = a[begin2++];}}while (begin1 <= end1){tmp[index++] = a[begin1++];}while (begin2 <= end2){tmp[index++] = a[begin2++];}//一趟排序完后,将有序序列拷贝到原数组中memcpy(a, tmp, sizeof(int) * index);}// 更新gap变为二倍gap *= 2;}free(tmp);tmp = NULL;
}归并排序的特性总结:
- 归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。
- 时间复杂度:O(N*logN)
- 空间复杂度:O(N)
- 稳定性:稳定
三、排序算法整体总结:
稳定性:指数组中相同元素在排序后相对位置不发生变化。
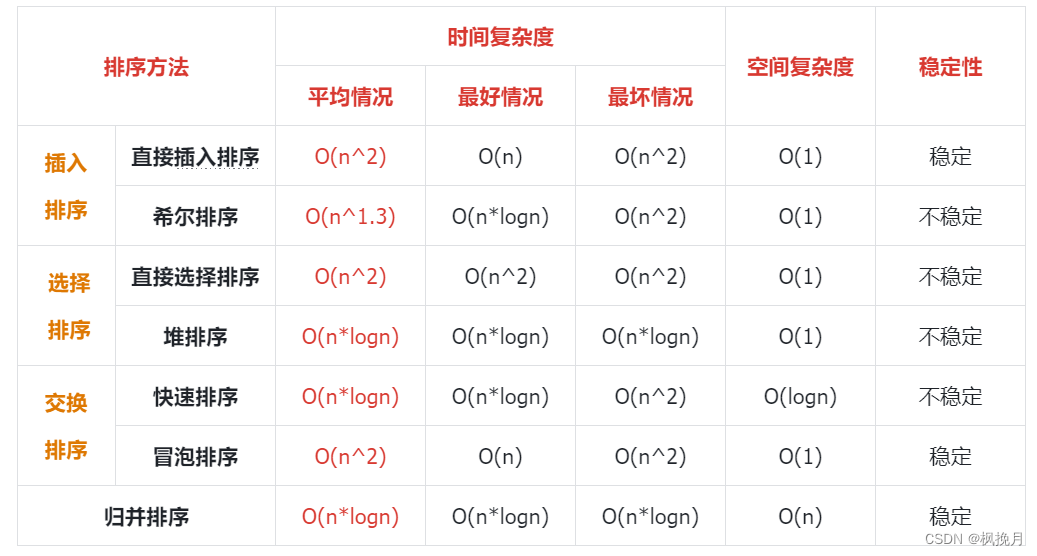
补充:
1、在希尔排序中,增量的选择会影响其时间复杂度。
2、序列初始顺序在一些算法中也会影响其时间复杂度。

