【Acwing 周赛复盘】第92场周赛复盘（2023.2.25）

周赛复盘 ✍️

本周个人排名：1293/2408

AC情况：1/3

这是博主参加的第七次周赛，又一次体会到了世界的参差（这次周赛记错时间了，以为 19:15 开始，不然 T3 应该也能 AC，就差一点 😂）

T1 签到题。✅

T2 没啥思路，就跳过去做 T3 了。❌ （经过y总讲解后，发现这是一道非常精妙，涉及树的前序遍历的递归题，值得反复咀嚼）

T3 题意有点绕，但是读明白之后，就是一道并查集的变形题目，但是融合了一点贪心思想。在看样例1时，以为只要输出最大集合的元素个数就行了；但是模拟样例2时发现，不对啊，这后面几个输出怎么和自己想的不一样呢。于是就开始模拟样例2的过程，但是中途却卡壳了许久，有几个输出一直没想明白。等完全想明白时，比赛时间已经到了。❌

希望未来也能继续努力，紧跟大佬们的步伐，继续加油 💪

周赛信息 📚

时间：2023年 2 月 25 日 19：00-20：15

竞赛链接： https://www.acwing.com/activity/content/2908/

y总直播间：http://live.bilibili.com/21871779

y总录播讲解视频：【AcWing杯 - 第 92 场周赛讲解】

题目列表 🧑🏻‍💻

题目名称	原题链接	视频讲解	难度
AcWing 4864. 多边形	原题链接	视频链接	简单 🟢
AcWing 4865. 有效类型	原题链接	视频链接	中等 🟡
AcWing 4866. 最大数量	原题链接	视频链接	困难 🔴

题解 🚀

【题目A】多边形

【题目描述】

如果一个正多边形的边数 $n$ 能被 $4$ 整除，那么就称该正多边形是美丽的。

现在，给定一个正多边形的边数 $n$，请你判断它是否是美丽的。

【输入】

第一行包含整数 $T$，表示共有 $T$ 组测试数据。

每组数据占一行，包含一个整数 $n$。

【输出】

每组数据输出一行结果，如果给定正多边形是美丽的，则输出 YES，否则输出 NO。

【数据范围】

前 $3$ 个测试点满足 $1\le T\le 10$。

所有测试点满足 $1\le T\le 10^4$，$3\le n\le 10^9$。

【输入样例1】

4
3
4
12
1000000000

【输出样例1】

NO
YES
YES
YES

【原题链接】

https://www.acwing.com/problem/content/4867/

---

【题目分析】

签到题。

【周赛现场 AC 代码】✅

#include<bits/stdc++.h>using namespace std;int T, x;int main() {cin >> T;while (T--) {cin >> x;if (x % 4 == 0)cout << "YES" << endl;elsecout << "NO" << endl;}return 0;
}

---

【题目B】有效类型

【题目描述】

在本题中，关于有效类型字符串，具体定义如下：

• int 是有效类型字符串。
• 如果字符串 X 和字符串 Y 都是有效类型字符串，则 pair<X,Y> 是有效类型字符串。

现有一行若干个单词，每个单词要么是 pair，要么是 int，并且其中 int 的数量恰好为 $n$ 个。

你可以在不改变单词顺序的前提下，在这一行中任意添加 <、>、, 符号。

你的任务是构造出一个有效类型字符串。

输出这个有效类型字符串。

注意：

1. 有效类型字符串中 不含 空格或其它多余字符。
2. 可以证明如果存在满足条件的有效类型字符串，那么它一定是唯一的。
3. 如果不存在满足条件的有效类型字符串，输出 Error occurred 即可。

【输入】

第一行包含整数 $n$，表示给定单词中 int 的数量。

第二行包含若干个单词，每个单词要么是 pair，要么是 int。

【输出】

输出满足条件的有效类型字符串，如果不存在，则输出 Error occurred。

注意，有效类型字符串中 不含 空格或其它多余字符。

【数据范围】

前 $6$ 个测试点满足：$1\le n\le 5$。
所有测试点满足：$1\le n\le 10^5$，输入的总单词数量不超过 $10^5$，输入的 int 数量恰好为 $n$。

【输入样例1】

3
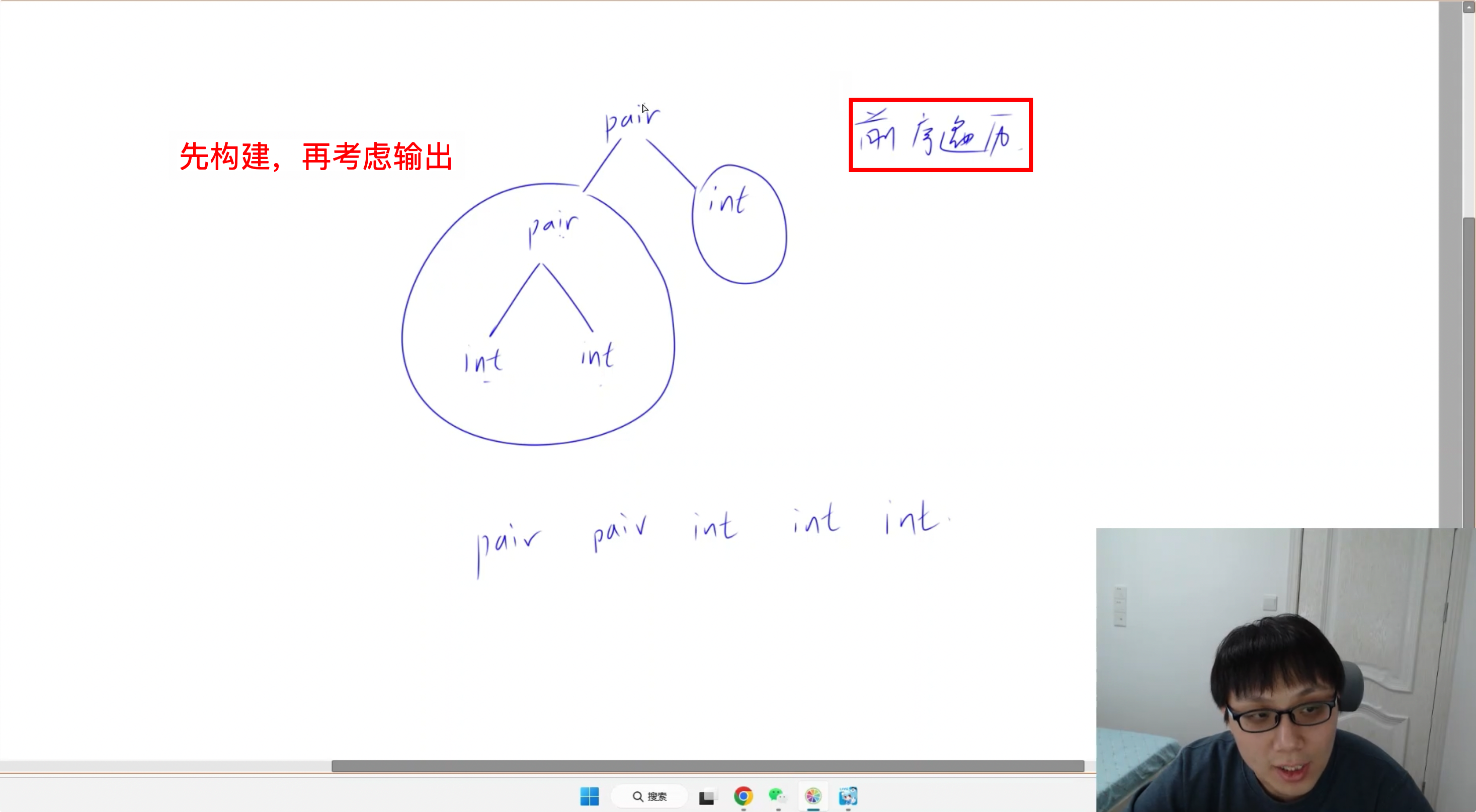
pair pair int int int

【输出样例1】

pair<pair<int,int>,int>

【输入样例2】

1
pair int

【输出样例2】

Error occurred

【原题链接】

https://www.acwing.com/problem/content/4868/

---

【题目分析】

递归构建 前序遍历的 pair 二叉树，代码十分精妙（详见代码注释）

这种递归的解题方式 值得反复咀嚼。

详细讲解见y总视频：https://www.acwing.com/video/4637/

【复盘后的优化代码】✅

//
// Created by Ricky X on 2023/2/24.
//#include<bits/stdc++.h>using namespace std;
int n;
string str, ans;bool dfs() {// 当前有字符可以读入if (cin >> str && str != "") {// 当前读入字符串为pair，则需要构建左右子树if (str == "pair") {ans += "pair<";if (!dfs()) return false; // 无法构建左子树，返回falseans += ",";if (!dfs()) return false; // 无法构建右子树，返回falseans += ">";return true;} else if (str == "int") {  // 读入为int，直接返回trueans += "int";return true;}} else {  // 当前没有字符读入，无法构建，返回falsereturn false;}
}int main() {cin >> n;// dfs()的作用是读入一个字符串，并且将其作为根结点，判断能否建立一颗树// dfs()返回true，说明当前读入的字符串可以构建一颗树// dfs()返回false，说明当前读入的字符串不可以构建一棵树// 不可以构建的情况：1.字符串读完了；2.读入pair，但是无法构建左右子树// dfs()构建成功，但是还有字符串读入，就会有多棵树，舍去该情况// 当且仅当dfs()构建成功，且没有字符串读入时，才能输出答案// 答案存储到字符串ans中bool flag = dfs();if (flag && cin >> str) flag = false;// 输出结果if (!flag) cout << "Error occurred" << endl;else cout << ans << endl;return 0;
}

【周赛现场 AC 代码】

现场未 AC

---

【题目C】最大数量

【题目描述】

一个无向图有 $n$ 个点，编号 $1\sim n$。

这些点之间没有任何边。

给定 $d$ 个需求，编号 $1\sim d$。

其中，第 $i$ 个需求是让点 $x_i$ 和点 $y_i$ 连通。

需求可能存在重复。

在本题中，你需要依次解决 $d$ 个问题，编号 $1\sim d$。

其中，第 $i$ 个问题是，请你在图中添加恰好 $i$ 条无向边（不能添加重边和自环），使得：

1. 前 $i$ 个需求都得到满足。
2. 所有点的度的最大值尽可能大。

对于每个问题，你不需要输出具体方案，你只需要输出度的最大可能值。

注意：

1. 如果点 $a$ 和点 $b$ 之间存在路径，则称点 $a$ 和点 $b$ 连通。
2. 图中与点 $a$ 关联的边数，称为点 $a$ 的度。
3. $d$ 个问题之间是相互独立的，每个问题的答案都必须独立计算。

【输入】

第一行包含两个整数 $n,d$。

接下来 $d$ 行，其中第 $i$ 行包含两个整数 $x_i,y_i$，表示第 $i$ 个需求是让点 $x_i$ 和点 $y_i$ 连通。

【输出】

共 $d$ 行，其中第 $i$ 行输出第 $i$ 个问题中，度的最大可能值。

【数据范围】

前三个测试点满足，$2\le n\le 10$。

所有测试点满足，$2\le n\le 1000$，$1\le d\le n-1$，$1\le x_i,y_i\le n$，$x_i\ne y_i$。

【输入样例1】

7 6
1 2
3 4
2 4
7 6
6 5
1 7

【输出样例1】

1
1
3
3
3
6

【输入样例2】

10 8
1 2
2 3
3 4
1 4
6 7
8 9
8 10
1 4

【输出样例2】

1
2
3
4
5
5
6
8

【原题链接】

https://www.acwing.com/problem/content/4869/

---

【题目分析】

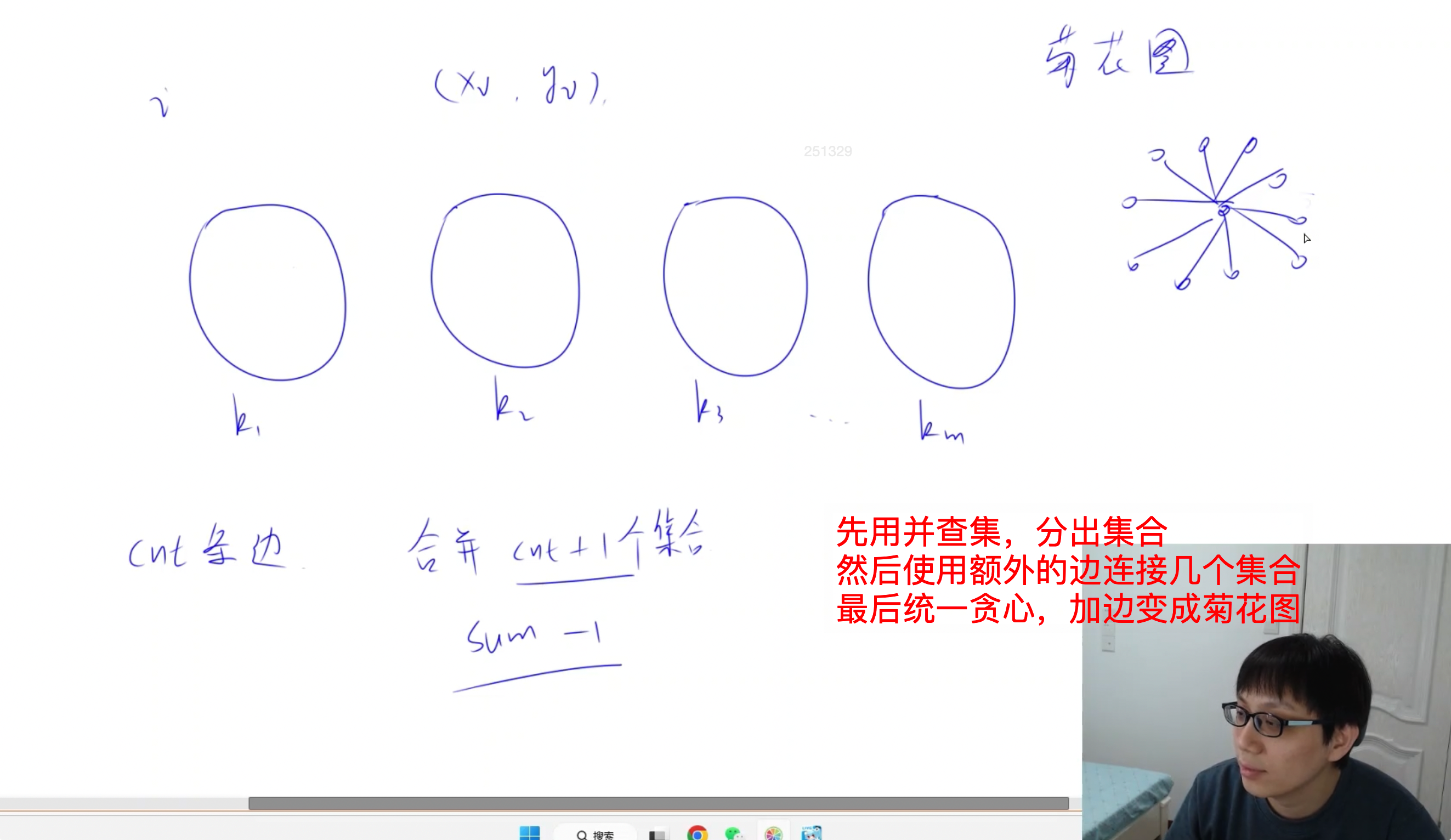
并查集 + 贪心（菊花图）

具体讲解见y总视频：https://www.acwing.com/video/4638/

【复盘后的优化代码】✅

//
// Created by Ricky X on 2023/2/24.
//#include<bits/stdc++.h>using namespace std;
const int N = 1010;
int pre[N], sum[N];
int n, d, a, b, op; // op是可以额外连接的操作次数// 并查集初始化
void init() {for (int i = 1; i <= n; i++) pre[i] = i, sum[i] = 1;
}// 查找元素x的祖先
int find(int x) {if (pre[x] != x) pre[x] = find(pre[x]);return pre[x];
}// 合并两个集合
void join(int a, int b) {int x = find(a);int y = find(b);if (x != y) pre[x] = y, sum[y] += sum[x];else op++; // 额外连接操作数+1
}// 查询
void solve() {// 将当前集合的大小存入vectorvector<int> v;v.clear();for (int i = 1; i <= n; i++)if (pre[i] == i)v.push_back(sum[i]);sort(v.begin(), v.end(), greater<int>());// 通过op次操作，把前op个元素数量最大的集合合并int res = v[0]; // 第一个最大的集合是不用合并的for (int i = 1; i <= op; i++) {res += v[i];}cout << res - 1 << endl;
}int main() {ios::sync_with_stdio(false);  //cin读入优化cin.tie(0);cin >> n >> d;init();for (int i = 1; i <= d; i++) {cin >> a >> b;join(a, b);solve();  // 求解当前问题i的答案}return 0;
}

---