做集团网站一年多少钱青岛专业网站制作
1.RSA
知道 flag.enc 和 pub.key,典型的加密、解密
将pub,key 改为pub.txt
打开后发现公钥

在RSA公私钥分解 Exponent、Modulus,Rsa公私钥指数、系数(模数)分解--查错网 进行解密
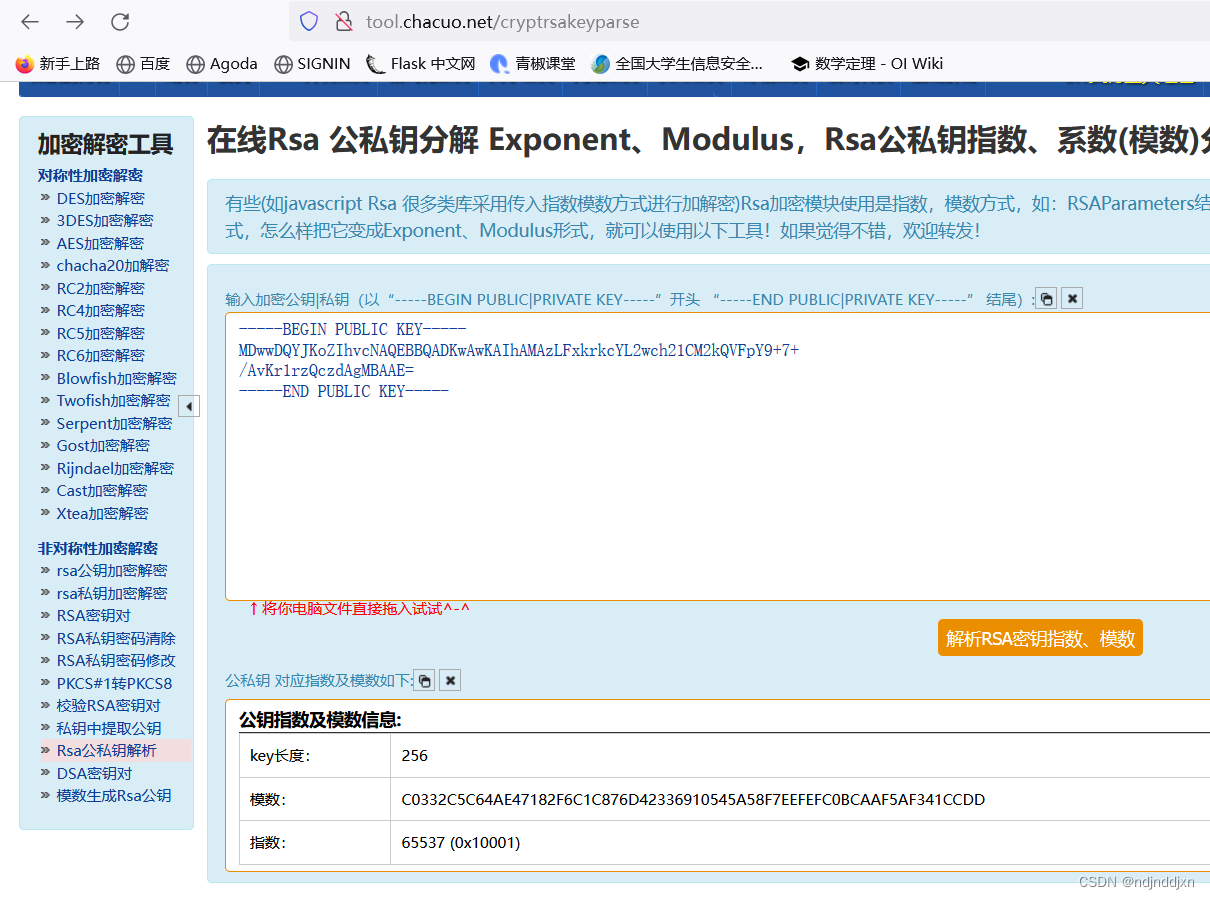
得到e=65537
n=86934482296048119190666062003494800588905656017203025617216654058378322103517
在python中转化,模数是16进制的n
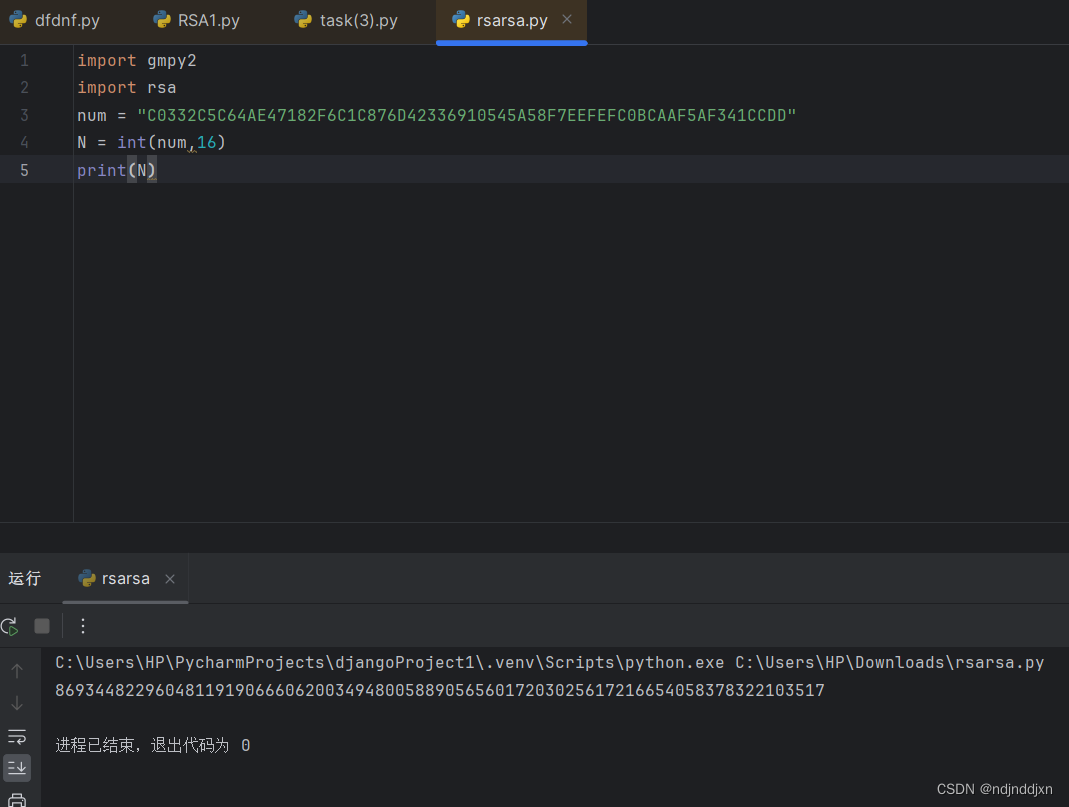
然后求p和q
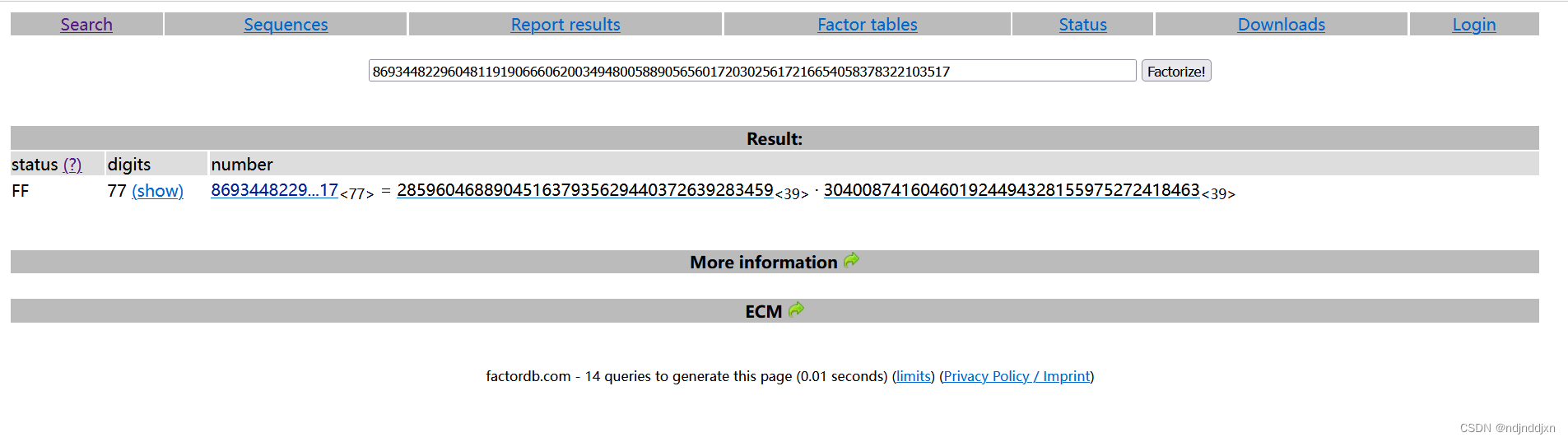
后面来编写脚本

import gmpy2
import rsa
num = "C0332C5C64AE47182F6C1C876D42336910545A58F7EEFEFC0BCAAF5AF341CCDD"
N = int(num,16)
E = 65537
p = 285960468890451637935629440372639283459
q = 304008741604601924494328155975272418463
D = int(gmpy2.invert(E,(p-1)*(q-1)))
privkey = rsa.PrivateKey(N, E, D, p, q)
with open("C:\\Users\\HP\\Desktop\\flag.enc", "rb+") as file:text = file.read()
message = rsa.decrypt(text,privkey)
print(N)
print(message)
代码核心:
从一个给定的公钥参数(N 和E)以及私钥的两个质数因子(p和 q)来创建一个 RSA 私钥,并使用这个私钥来解密一个文件。
代码首先导入 gmpy2和 rsa 模块,然后定义了一系列变量,包括公钥的模数 N、公钥的指数 E、两个质数 p,q,以及通过 gmpy2.invert 函数计算出的私钥指数 D。
接下来创建一个rsa.PrivateKey 对象,并尝试打开一个加密文件来读取其内容。解密后的消息被存储在 message变量中,最后打印出公钥的模数 N 和解密后的消息。
补充:
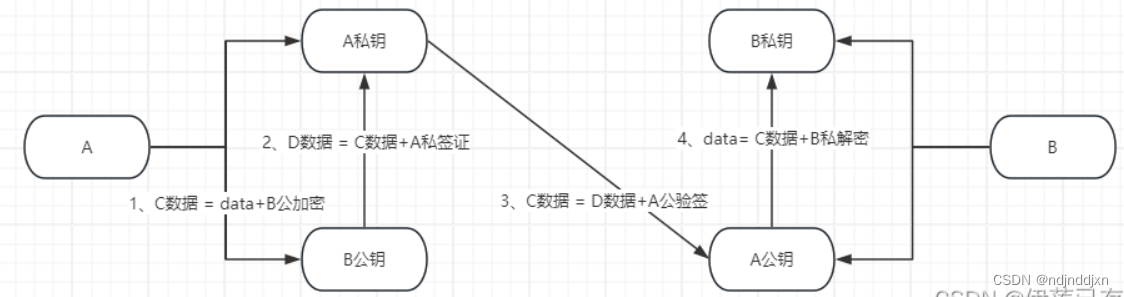
RSA 加密/解密
在 RSA 加密/解密过程中,公钥用于加密数据,私钥用于解密数据。在这个例子中,你已经使用了公钥的模数 N 和指数 E 来模拟(尽管没有实际加密过程)公钥,并用私钥的质数因子 p和 q 来计算私钥指数 D,然后用这个私钥来解密一个文件。
RSA 签名/验证签名
在 RSA 签名/验证签名过程中,私钥用于生成签名,公钥用于验证签名。签名通常附加在原始消息之后,以证明消息的真实性和完整性。
使用 RSA 私钥生成签名的过程大致如下:
- 发送者使用哈希函数(如 SHA-256)对原始消息进行哈希处理,得到一个固定长度的哈希值。
- 发送者使用其 RSA 私钥和哈希算法对哈希值进行签名,生成一个签名值。
- 发送者将原始消息和签名值一起发送给接收者。
有wp说,这一题属于签名(公钥加签),但是这是错误的,只有拥有私钥的A才能生成有效的签名,所以签名可以作为A的身份验证,这是没有涉及RSA签名及验证,
我们一般说地加签和减签,是说公钥解签,私钥加签
公钥解签:
当发送者(例如A)想要发送一条消息给接收者(例如B)并确保消息的真实性和完整性时,A会使用自己的私钥对消息进行签名。这个过程通常涉及对消息的哈希值进行加密,生成一个签名。
A将原始消息和签名一起发送给B
私钥加签:
B收到消息和签名后,使用A的公钥对签名进行解密,得到原始消息的哈希值。
B同时会对原始消息进行哈希运算,得到另一个哈希值。
如果B使用A的公钥解密签名得到的哈希值和B自己对原始消息进行哈希运算得到的哈希值相同,那么B就可以确认这条消息是由A发送的,并且没有被篡改。
2.RSARoll
根据题目:
RSA roll!roll!roll!Only number and a-z(don't use editor which MS provide)
先来查一下什么叫Roll?
这里说得是Roll按行加密,
前面两个 数n,e,后面是密文c
提醒:不要总是觉得 密文C 就是一连串的字符串,密文C 也可以是分行的,记住不要把分行符删除让 密文C 变为一个字符串。应该按行进行解密
来上脚本
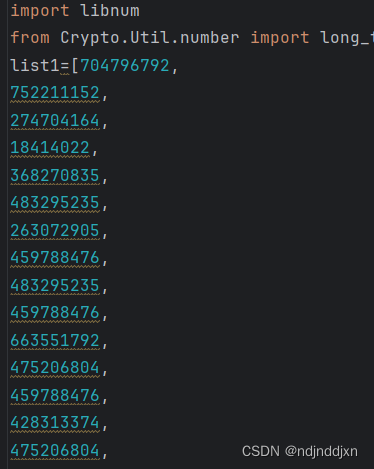
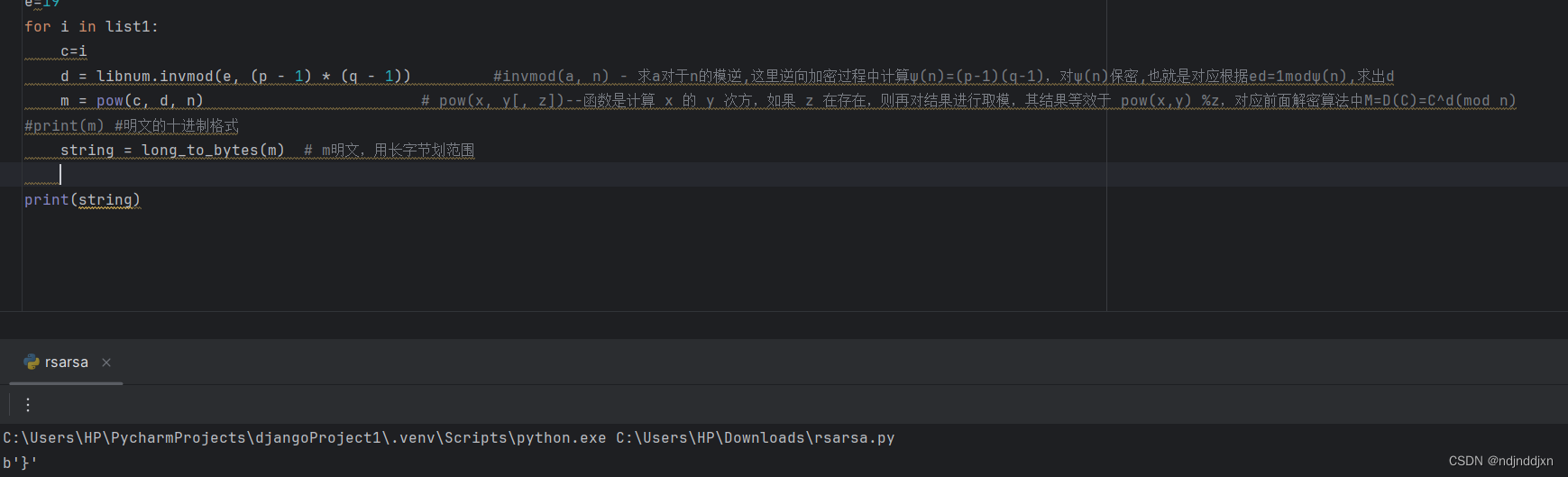
直接输出string,只得到},分析一下,它算了很多次私钥,每一次都使用的d都相同,
虽然没有错误,但引起了混淆
我们修改一下,加上一段
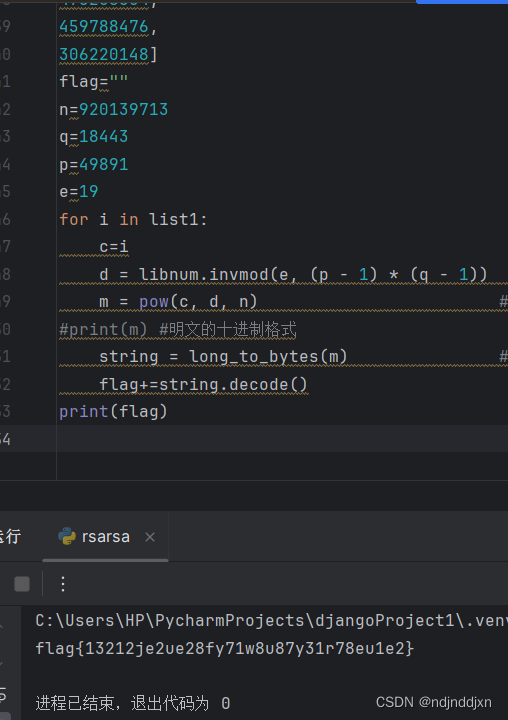
flag+=string.decode()将每个解密后的字符串追加到flag变量中。这假设了每个密文解密后都直接对应一段可读的文本,并且这些文本片段应该连续拼接。这在实际应用中可能并不总是正确的,特别是如果明文在加密前经过了某种形式的分割或编码.
较好的代码为:
import libnum
from Crypto.Util.number import long_to_byteslist1 = [# ... 你的密文列表 ...
]n = 920139713
q = 18443
p = 49891
e = 19# 计算私钥的d部分,只需要做一次
phi_n = (p - 1) * (q - 1)
d = libnum.invmod(e, phi_n)for i in list1:c = i# 使用相同的d来解密所有的cm = pow(c, d, n)# 可能需要处理填充或转换,这里只是简单地将整数转换为字节string = long_to_bytes(m)print(string)

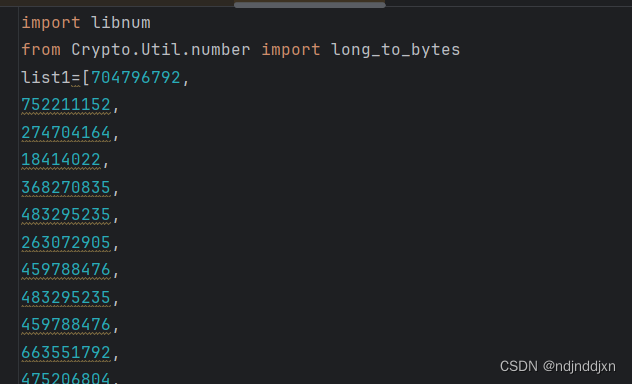
结果:

合起来就可了
补充:
欧几里得算法

主要运用在计算模逆元(或乘法逆元)
详细在中国剩余定理 - OI Wiki
