手机记事本做网站竞价培训班
数论
整数的整除性
- [x]表示不超过x的最大整数,叫做取整函数或高斯函数。
- 设整数a,b不同时为零,则存在一对整数m,n,使得 ( a , b ) = a m + b n (a, b) = am + bn (a,b)=am+bn。注:a和b的最大公因数会写成 (a, b) 的形式,最小公倍数会写成 [a, b] 的形式。
- 若 a ∣ b c a\ |\ bc a ∣ bc,且 ( a , b ) = 1 (a, b) = 1 (a,b)=1,则 a ∣ c a\ |\ c a ∣ c。
- 设p为素数,若 p ∣ a b p\ |\ ab p ∣ ab,则 p ∣ a p\ |\ a p ∣ a,或 p ∣ b p\ |\ b p ∣ b。推论:设p为素数,若 p ∣ a 1 a 2 . . . a k p\ |\ a_1a_2...a_k p ∣ a1a2...ak,则存在 a i ( 1 ≤ i ≤ k ) a_i(1\le i \le k) ai(1≤i≤k),使得 p ∣ a i p\ |\ a_i p ∣ ai。
- ( a , b ) [ a , b ] = ∣ a b ∣ (a, b)[a, b] = |ab| (a,b)[a,b]=∣ab∣.
- 求多个整数的最大公因数,可以这样转化:(a, b, c) = ((a, b), c)。求多个整数的最大公倍数,可以转化为:[a, b, c] = [[a, b], c]。
- 算术基本定理:任何大一1的整数可以分解成素因数乘积的形式,并且,如果不计分解式中素因数的次序,这种分解式是惟一的。
- 一般地,对给定的两个大于1的整数a, b,找出它们所有的互异素因数,然后将a, b表示成这些素因数的幂的乘积,如果其中一个素因数在a或b中不出现,就将这个素因数的幂指数写作0,那么(a, b)可以表示成这些素因数的幂的乘积,每个素因数的幂指数为其在a与b中的幂指数的最小者,而[a, b]也可以表示成这些素因数幂的乘积,每个素因数的幂指数为其在a与b的幂指数的最大者.
同余
- a ≡ b ( m o d n ) ⇔ n ∣ a − b a\equiv b(mod\ n)\Leftrightarrow n|a-b a≡b(mod n)⇔n∣a−b.
- 若 a ≡ b ( m o d n ) a\equiv b(mod\ n) a≡b(mod n),且 c ≡ d ( m o d n ) c\equiv d(mod\ n) c≡d(mod n),则
- a + c ≡ b + d ( m o d n ) a+c\equiv b+d(mod\ n) a+c≡b+d(mod n);
- a c ≡ b d ( m o d n ) ac\equiv bd(mod\ n) ac≡bd(mod n)
- k a ≡ k b ( m o d n ) ka\equiv kb(mod\ n) ka≡kb(mod n),k为任意整数
- a m ≡ b m ( m o d n ) a^m \equiv b^m(mod\ n) am≡bm(mod n),m为正整数
- 若 a b ≡ a c ( m o d n ) ab\equiv ac(mod\ n) ab≡ac(mod n),且 ( a , n ) = 1 (a, n) = 1 (a,n)=1,则 b ≡ c ( m o d n ) b\equiv c(mod\ n) b≡c(mod n).
- 我们把所有与整数a模n同余的整数构成的集合叫做模n的一个剩余类,记作[a],并把a叫做剩余类[a]的一个代表元。
- a ≡ b ( m o d n ) ⇔ [ a ] = [ b ] . a\equiv b(mod\ n) \Leftrightarrow [a] = [b]. a≡b(mod n)⇔[a]=[b].
- 剩余类加法: [ a ] + [ b ] = [ a + b ] [a] + [b]=[a+b] [a]+[b]=[a+b]。剩余类乘法: [ a ] [ b ] = [ a b ] [a][b]=[ab] [a][b]=[ab]。
- [0]叫剩余类环的零元,[1]叫剩余类环的单位元。若 [ a ] + [ b ] = [ b ] + [ a ] = [ 0 ] [a]+[b]=[b]+[a]=[0] [a]+[b]=[b]+[a]=[0],则称[b]为[a]的负元。若 [ a ] [ b ] = [ b ] [ a ] = [ 1 ] [a][b]=[b][a]=[1] [a][b]=[b][a]=[1],则称[b]为[a]的逆元。
- 非零元[a]有逆元的充要条件是 ( a , n ) = 1 (a, n)=1 (a,n)=1。n就是剩余类定义里面的那个n。
- 在模n的剩余类环中,若[a]存在逆元,则它的逆元仅有一个。
- 无零因子:任意两个非零整数的乘积不等于0。但是,剩余类乘法中并不都满足这个条件。比如模6的剩余类乘法, [ 2 ] [ 3 ] = 0 [2][3]=0 [2][3]=0。但是模5的剩余类环无零因子。
- 设m为素数,a为任意整数,且 ( a , m ) = 1 (a, m)=1 (a,m)=1,则 a m − 1 ≡ 1 ( m o d m ) a^{m-1}\equiv 1(mod\ m) am−1≡1(mod m).
- 欧拉定理:设 m 为正整数,a 为任意整数,且 ( a , m ) = 1 (a, m) = 1 (a,m)=1,则: a ϕ ( m ) ≡ 1 ( m o d n ) a^{\phi(m)}\equiv 1(mod\ n) aϕ(m)≡1(mod n),其中 ϕ ( m ) \phi(m) ϕ(m)表示1,2,3,…,m 中与m互素的正整数的个数。若在算数基本定理中, N = p 1 a 1 ∗ p 2 a 2 ∗ … ∗ p m a m N=p_1^{a_1}*p_2^{a_2}*…*p_m^{a_m} N=p1a1∗p2a2∗…∗pmam,则: φ ( N ) = N ∗ p 1 − 1 p 1 ∗ p 2 − 1 p 2 ∗ … ∗ p m − 1 p m \varphi(N)=N*\frac{p_1 - 1}{p_1}∗\frac{p_2−1}{p_2}∗…∗\frac{p_m−1}{p_m} φ(N)=N∗p1p1−1∗p2p2−1∗…∗pmpm−1。不过要指出的是, φ ( 1 ) = 1 \varphi(1)=1 φ(1)=1。
- 一次同余方程 a x ≡ b ( m o d n ) ax\equiv b(mod\ n) ax≡b(mod n)有解,则 ( a , n ) ∣ b (a, n)|b (a,n)∣b。反过来,当 ( a , n ) ∣ b (a, n)|b (a,n)∣b,一次同余方程 a x ≡ b ( m o d n ) ax\equiv b(mod\ n) ax≡b(mod n)恰有(a, n)个解。
- b a % p = b ∗ a − 1 % p = b ∗ a p − 2 % p \frac{b}{a} \ \% \ p = b * a^{-1} \ \% \ p = b * a^{p-2} \ \% \ p ab % p=b∗a−1 % p=b∗ap−2 % p
一次不定方程
- 二元一次不定方程 a x + b y = c ax+by=c ax+by=c有解,等价于 ( a , b ) ∣ c (a, b)|c (a,b)∣c。
- 设 ( a , b ) = 1 (a, b)=1 (a,b)=1,则不定方程ax+by=c的整数通解为 { x = x 0 + b t y = y 0 − a t \begin{cases}x=x_0+bt\\y=y_0-at\end{cases} {x=x0+bty=y0−at其中t为任意整数, x = x 0 , y = y 0 x=x_0,y=y_0 x=x0,y=y0为不定方程 a x + b y = c ax+by=c ax+by=c的一个特解。
- 三元一次不定方程 a x + b y + c z = d ax+by+cz=d ax+by+cz=d有整数解的充要条件是 ( a , b , c ) ∣ d (a,b,c)|d (a,b,c)∣d
原根与指数
原根
- 设(a,m) = 1,则
(i)存在正整数n, 1 ≤ r < m 1≤ r< m 1≤r<m,使 a n = 1 a^n= 1 an=1(mod m);
(ii)设n为(i)中最小的正整数,则对整数k和l,同余式 a k = a l ( m o d m ) a^k=a^l(mod\ m) ak=al(mod m) 成立的充分必要条件是 k ≡ l ( m o d n ) k\equiv l(mod\ n) k≡l(mod n).特别地, a k = 1 ( m o d m ) a^k= 1(mod\ m) ak=1(mod m)成立的充分必要条件为n|k. - 对与m互素的整数a,满足 a n = 1 ( m o d m ) a^n= 1(mod\ m) an=1(mod m)的最小正整数n,称为a模m的阶.
组合数学
组合数
- 一个组合数是否为奇数: C ( n , k ) C(n,k) C(n,k)为奇数时, n & k = k n\&k=k n&k=k 。
- 令 a n = ∑ x = 0 N C N x ∗ 2 x a_n =\sum_{x=0}^NC_N^x*2^x an=∑x=0NCNx∗2x: a 0 = 1 a_0 =1 a0=1, a n = 3 ∗ a n − 1 a_n = 3*a_{n-1} an=3∗an−1。
求和公式
1.平方和公式
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-SemLiPww-1686468029027)(null)]
2.立方和公式
∑ i = 1 n i 3 = 1 3 + 2 3 + . . . + n 3 = n 2 ( n + 1 ) 2 4 = [ n ( n + 1 ) 2 ] 2 \sum\limits_{i = 1}^{n} i^3= 1^3 + 2 ^ 3 + ... + n^3 = \frac{n^2(n+1)^2}{4}=[\frac{n(n+1)}{2}]^2 i=1∑ni3=13+23+...+n3=4n2(n+1)2=[2n(n+1)]2
微积分
积分表
- 积分表1:
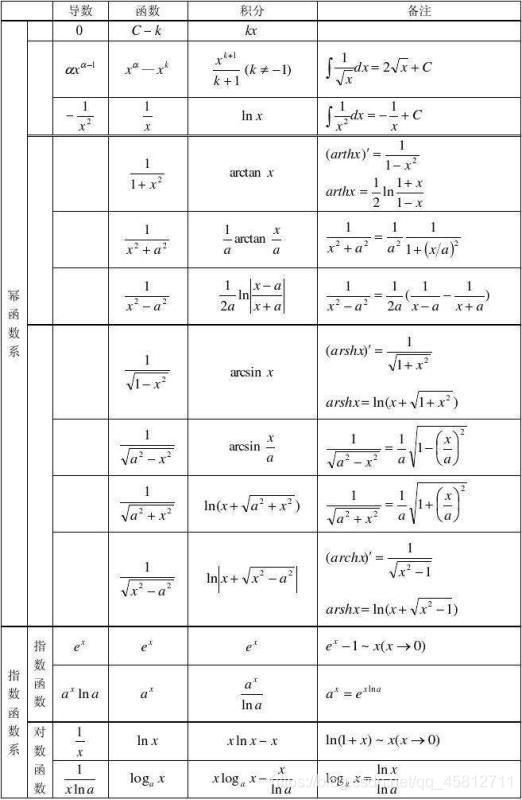
- 积分表2:

- 积分表3:
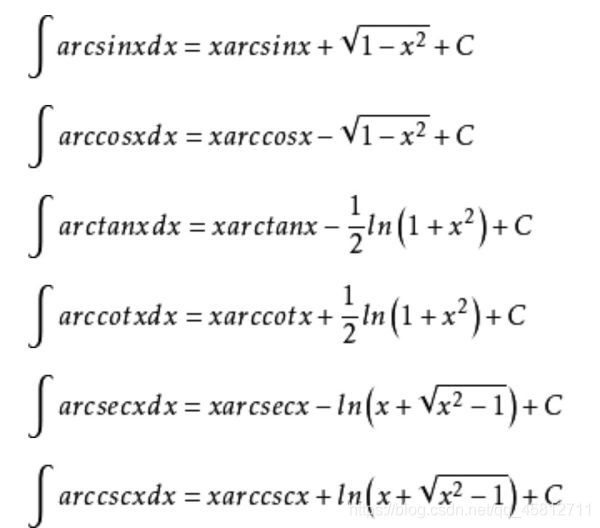
π \pi π 的值
- 不用记住准确值,一行代码就可以了呀。把这个放在main函数外面也是没问题的。
const double PI = acos(-1);
其他
- 在数学中,以Kenneth E. Iverson命名的“艾佛森括号”,是一种用方括号记号,如果方括号内的条件满足则为1,不满足则为0。
- 格雷码规则:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-NC5Ypxxs-1686468028452)(file:///D:\1398687709\1398687709\Image\C2C\3144C8683FBA94C26F58702AA73A398E.png)]
